本文旨在对斐波那契数组的算法实现做一个讲解
你真的懂斐波那契数列算法吗？
本章测试链接 : https://leetcode.cn/problems/fibonacci-number/
什么是斐波那契数列
斐波那契数列（Fibonacci sequence），又称黄金分割数列，是由意大利数学家莱昂纳多·斐波那契（Leonardo Fibonacci）以兔子繁殖为例子引入的数列。其数值为：1、1、2、3、5、8、13、21、34……在数学上，这一数列以如下递推的方法定义：
F(0)=0，F(1)=1，F(n)=F(n-1)+F(n-2)（n ≥ 2，n ∈ N*）。
斐波那契数列的算法实现
递归实现
这也是最容易想到的实现方式, 绝大部分人第一时间想到的就是这个实现方式, 也是最简单最易写的实现方式:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
int fib(int n) {
if (n == 0)
{
return 0;
}
if (n == 1)
{
return 1;
}
return fib(n - 1) + fib(n - 2);
}
};
测试结果如图(leetcode):
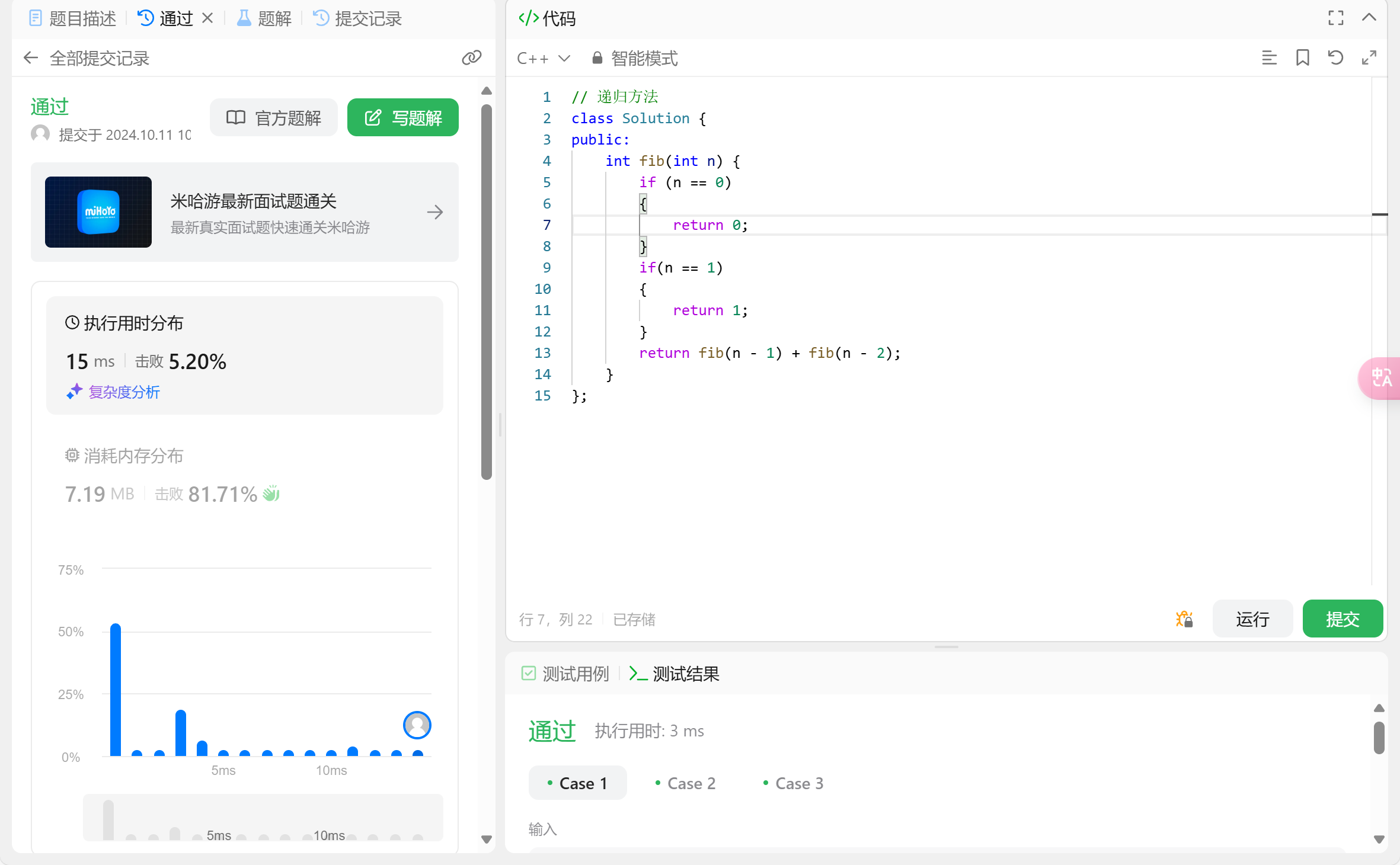因为其时间复杂度为O(2^n), 所以从图片上看起来执行速度非常慢, 因此我是非常不推荐去使用的。
动态规划实现
这是一种用空间来换时间的实现方式, 其时间复杂度为O(n), 其分为三种是实现方式:
- 自下而上
- 自上而下
- 空间优化(自上而下)
1.自下而上
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
vector<int> dp; // 反向dp处理
int f(int i)
{
if (i == 0)
{
return 0;
}
if (i == 1)
{
return 1;
}
if (dp[i] != -1)
{
return dp[i];
}
int ans = f(i - 1) + f(i - 2);
dp[i] = ans;
return ans;
}
int fib(int n) {
dp = vector<int>(n + 1, -1);
return f(n);
}
};
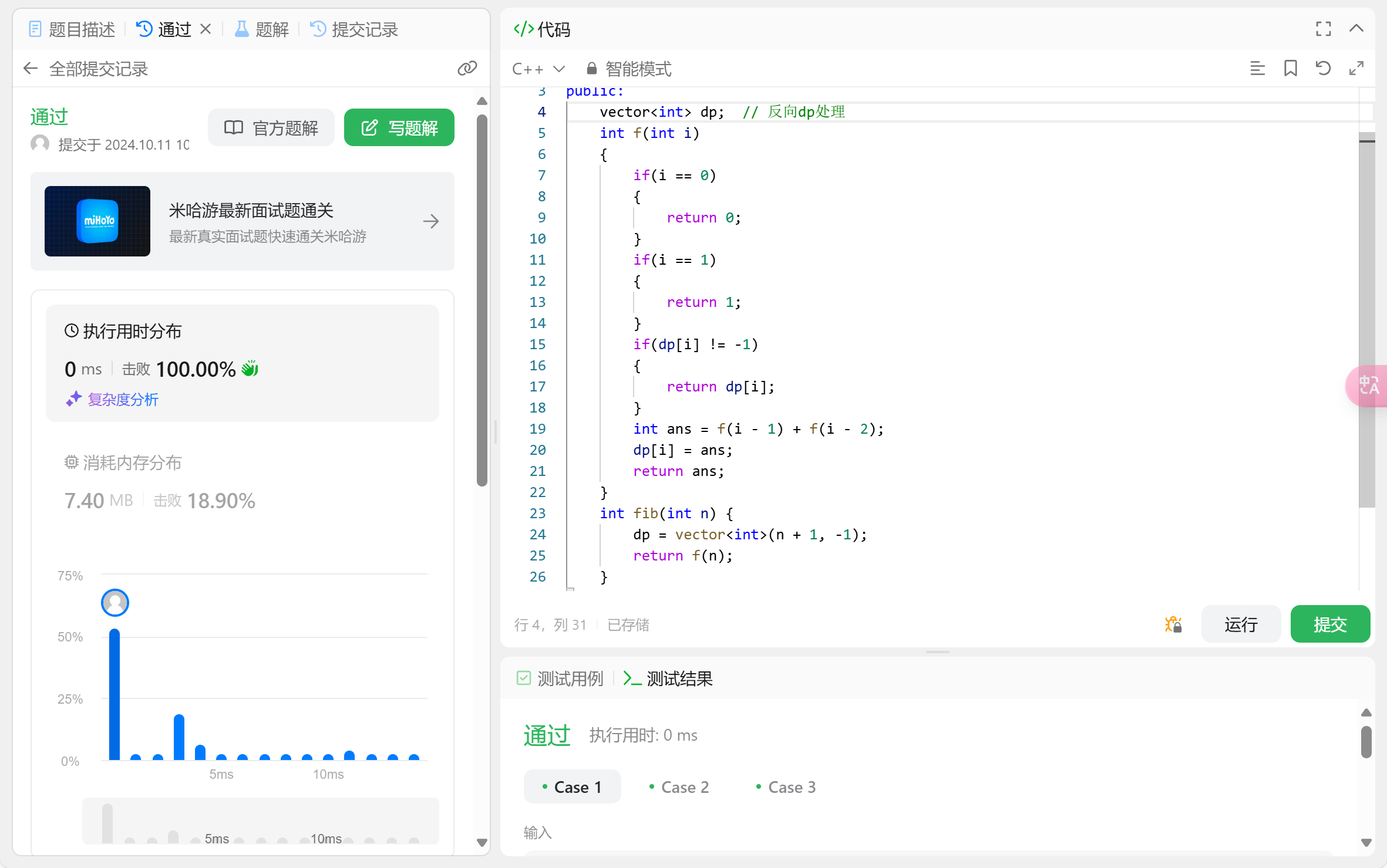
2.自上而下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
vector<int> dp;
int fib(int n) {
if (n == 0)
{
return 0;
}
if (n == 1)
{
return 1;
}
dp = vector<int>(n + 1, 0);
dp[1] = 1;
for (int i = 2; i <= n; ++i) // 使用for循环做正向处理
{
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
};
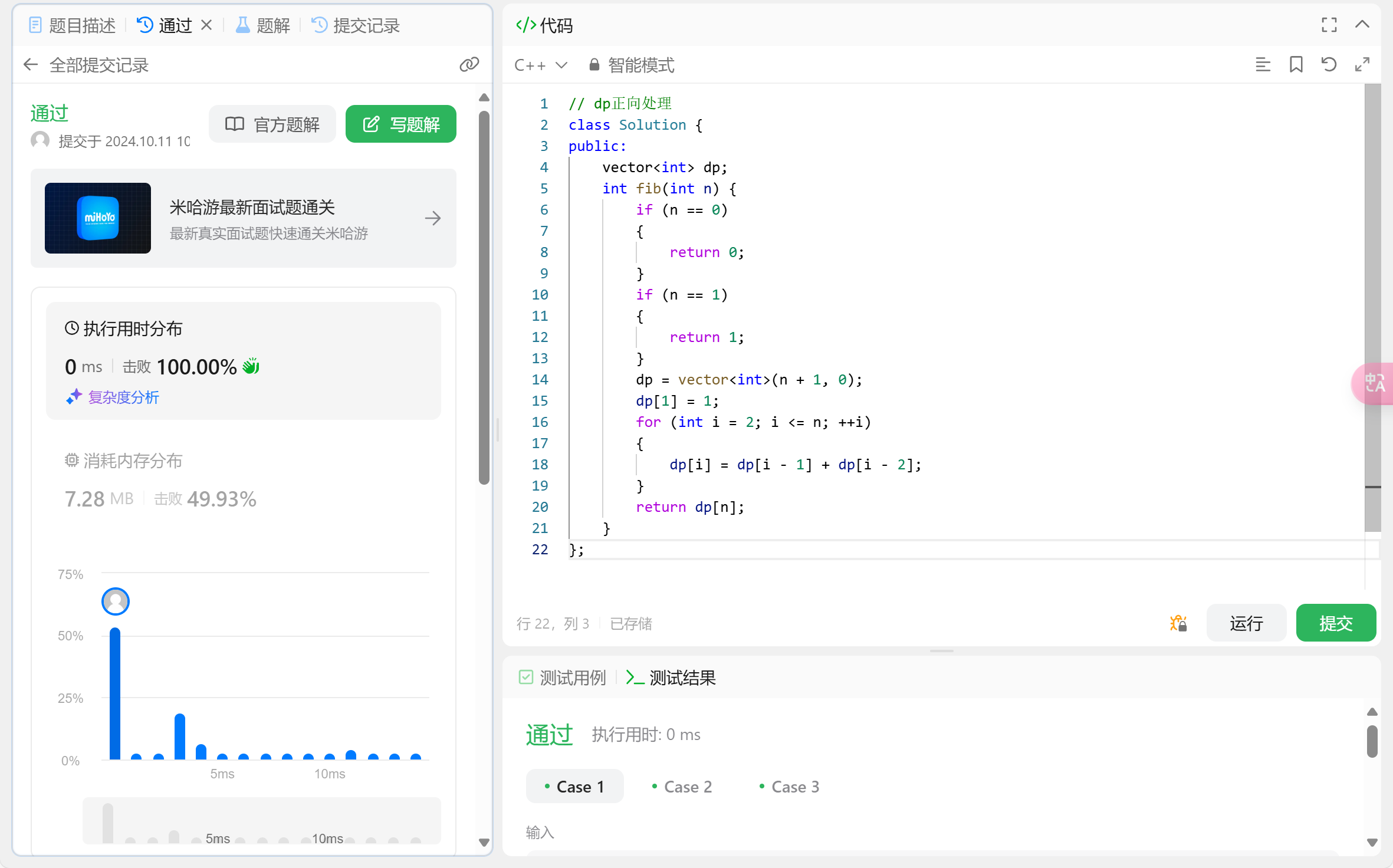
3.空间优化(自上而下)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
int lastLast, last; // 双变量代替dp, 实现对空间的优化
int fib(int n) {
if (n == 0)
{
return 0;
}
if (n == 1)
{
return 1;
}
lastLast = 0;
last = 1;
for (int i = 2, tmp; i <= n; ++i)
{
tmp = last;
last = last + lastLast;
lastLast = tmp;
}
return last;
}
};
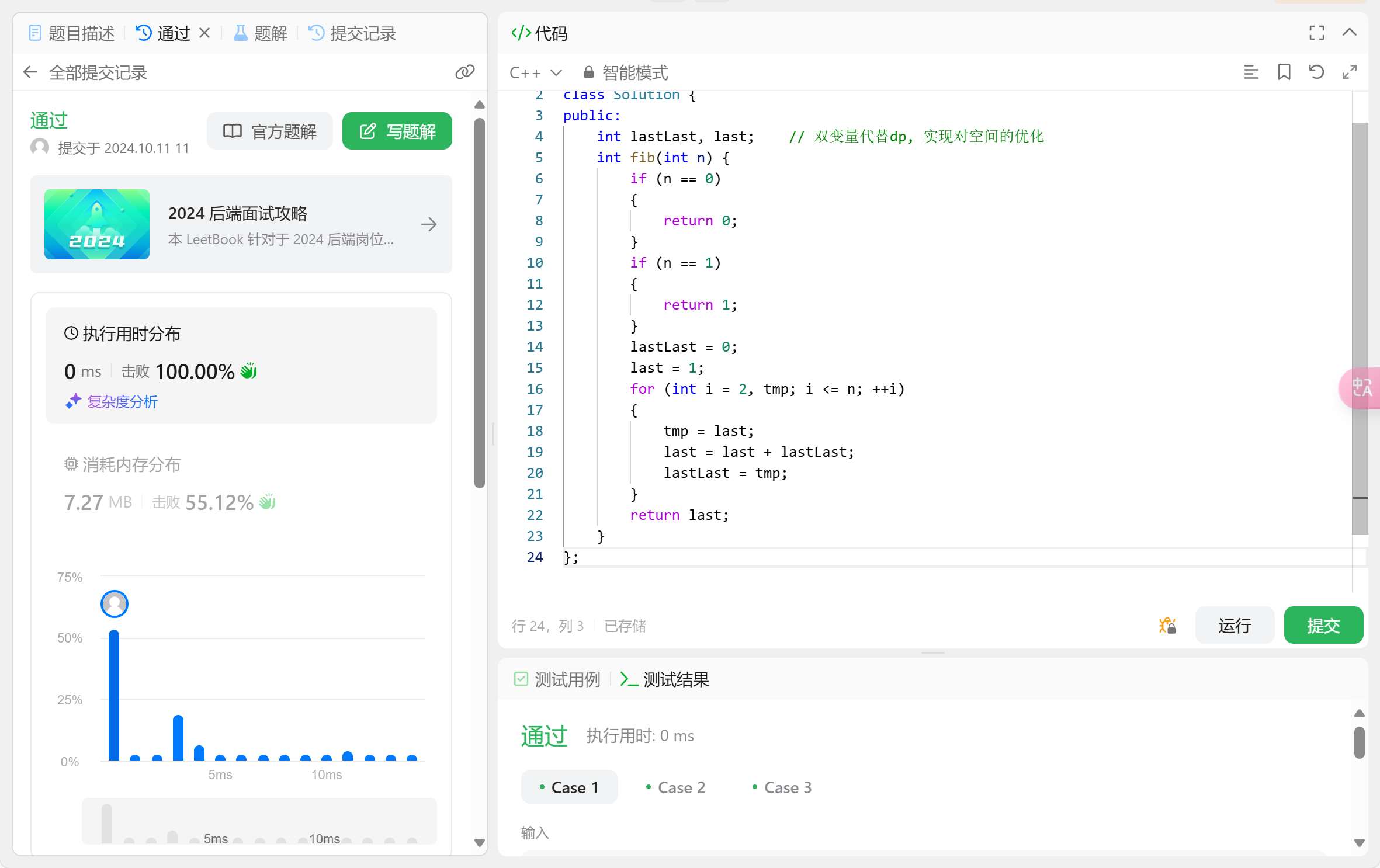
这三种方法:
第一种使用递归+反向dp
第二种使用正向dp
第三种使用双变量代替dp优化空间
但不论哪一种, 其时间复杂度都是O(n), 在数据测试中0ms没有任何压力, 实现代码也都不难, 是大部分参加算法竞赛的参赛者最常用的实现方式。
矩阵快速幂实现
这应该是本章最难的部分了, 其时间复杂度为O(logn), 应该是目前最快的实现斐波那契数列算法之一, 其实现方式如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
public:
// 矩阵乘法
vector<vector<long long>> mult(vector<vector<long long>>& a, vector<vector<long long>>& b) {
vector<vector<long long>> res(2, vector<long long>(2, 0));
// 两个二维矩阵的运算法则
res[0][0] = a[0][0] * b[0][0] + a[0][1] * b[1][0];
res[0][1] = a[0][0] * b[0][1] + a[0][1] * b[1][1];
res[1][0] = a[1][0] * b[0][0] + a[1][1] * b[1][0];
res[1][1] = a[1][0] * b[0][1] + a[1][1] * b[1][1];
return res;
}
// 矩阵快速幂
vector<vector<long long>> matrixPow(vector<vector<long long>> a, int n) {
vector<vector<long long>> result = { {1, 0}, {0, 1} }; // 单位矩阵
while (n > 0) {
if (n & 1) {
result = mult(result, a);
}
a = mult(a, a);
n >>= 1;
}
return result;
}
// 计算第n个斐波那契数
int fib(int n) {
if (n == 0) return 0;
vector<vector<long long>> base = { {1, 1}, {1, 0} };
vector<vector<long long>> result = matrixPow(base, n - 1);
return result[0][0];
}
};
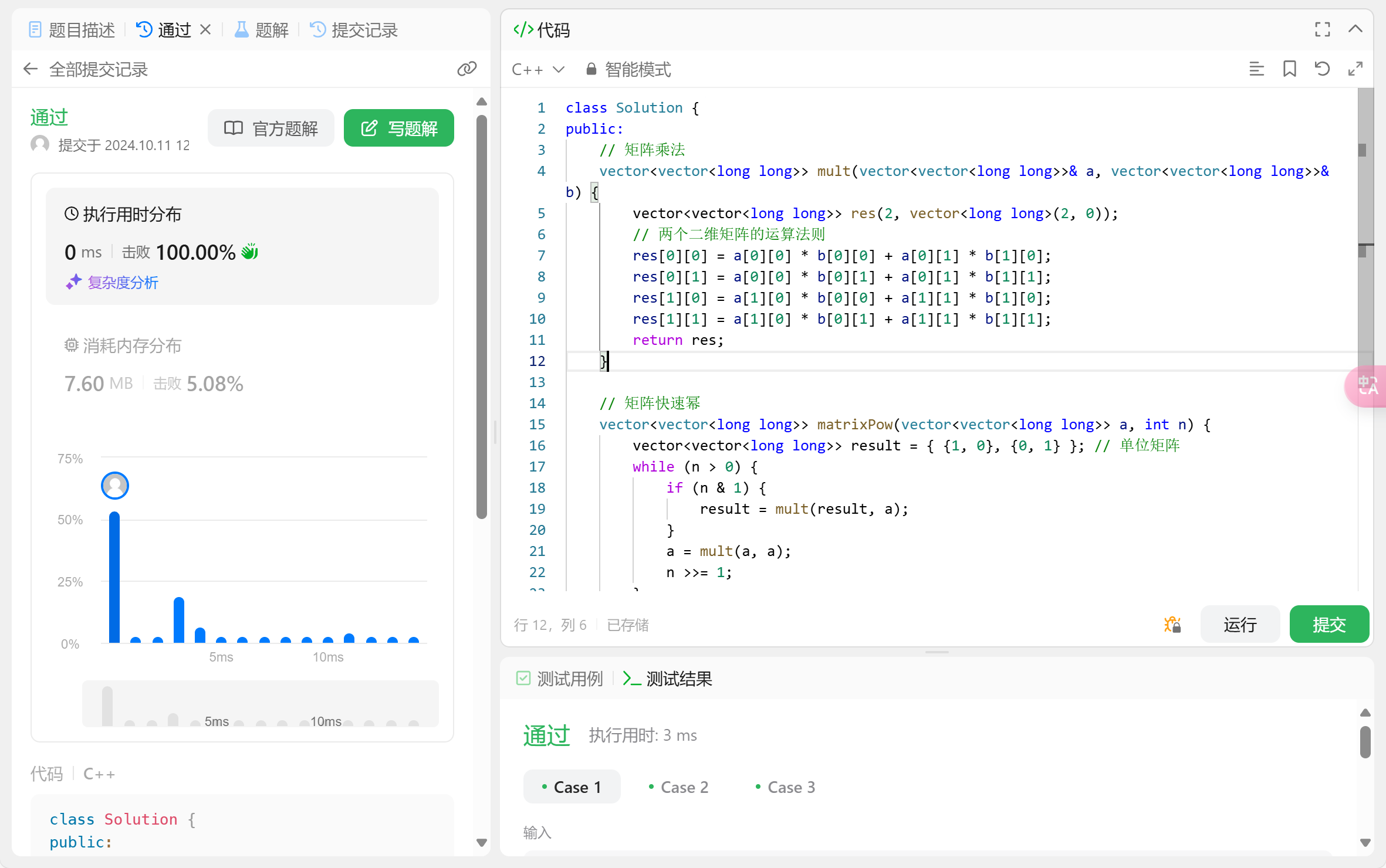注: 因为其时间复杂度为O(logn), 而O(n)就已经是0ms所以没有在测试中展现出来其优越性。
因为其构建矩阵有开销, 所以在数据大时的其优越的时间复杂度才会展现, 所以在数据量小时, 其反而会比其他实现方式慢(在数据量小时, 使用的动态规划的实现方式会更好)
其他实现
除了斐波那契数列的普通公式外, 还有一种公式:
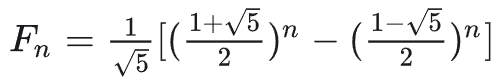(摘自文章: https://zhuanlan.zhihu.com/p/26679684)
使用这种实现方式可以将时间复杂度降到O(1), 我在这边就不做代码演示了, 有需要可自行查看。
总结
以上就是我关于斐波那契数列算法实现的讲解, 希望能够让你对斐波那契数列有更深的了解。
