让我们走向dp的世界
本章测试链接 :
https://leetcode.cn/problems/minimum-path-sum/description/
什么是dp
dp 是 Dynamic Programming, 中文翻译为动态规划, 其核心思想是通过将原问题分解为一系列重叠的子问题,逐步解决这些子问题并存储其结果,以避免重复计算, 提升算法效率, 本质是一种用空间换时间的算法思想。
dp的正确实现路径
很多人一见到dp就会想到重叠子问题和最优子结构, 无后效性等概念, 这些虽然很重要但其实对我们刚开始的学习帮助并不大。
真正的dp学习实现路径应该是以我们最熟悉的递归开始走向dp。
下面我将展示从递归走向dp的完整实现思路, 这边我使用leetcode的二维dp题目为例:
1. 做开始的递归实现
这是非常简单的递归实现, 我这边直接上代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include<climits>
#include<algorithm>
// 递归处理
class Solution {
public:
int n, m;
// 从终点往回推
int f(vector<vector<int>>& grid, int i, int j)
{
if (i == 0 && j == 0) return grid[0][0];
int up = INT_MAX;
int left = INT_MAX;
if (i - 1 >= 0)
{
up = f(grid, i - 1, j); // 向上走一步
}
if (j - 1 >= 0)
{
left = f(grid, i, j - 1); // 向左走一步
}
return grid[i][j] + min(up, left);
}
int minPathSum(vector<vector<int>>& grid) {
n = grid.size();
m = grid[0].size();
return f(grid, n - 1, m - 1);
}
};
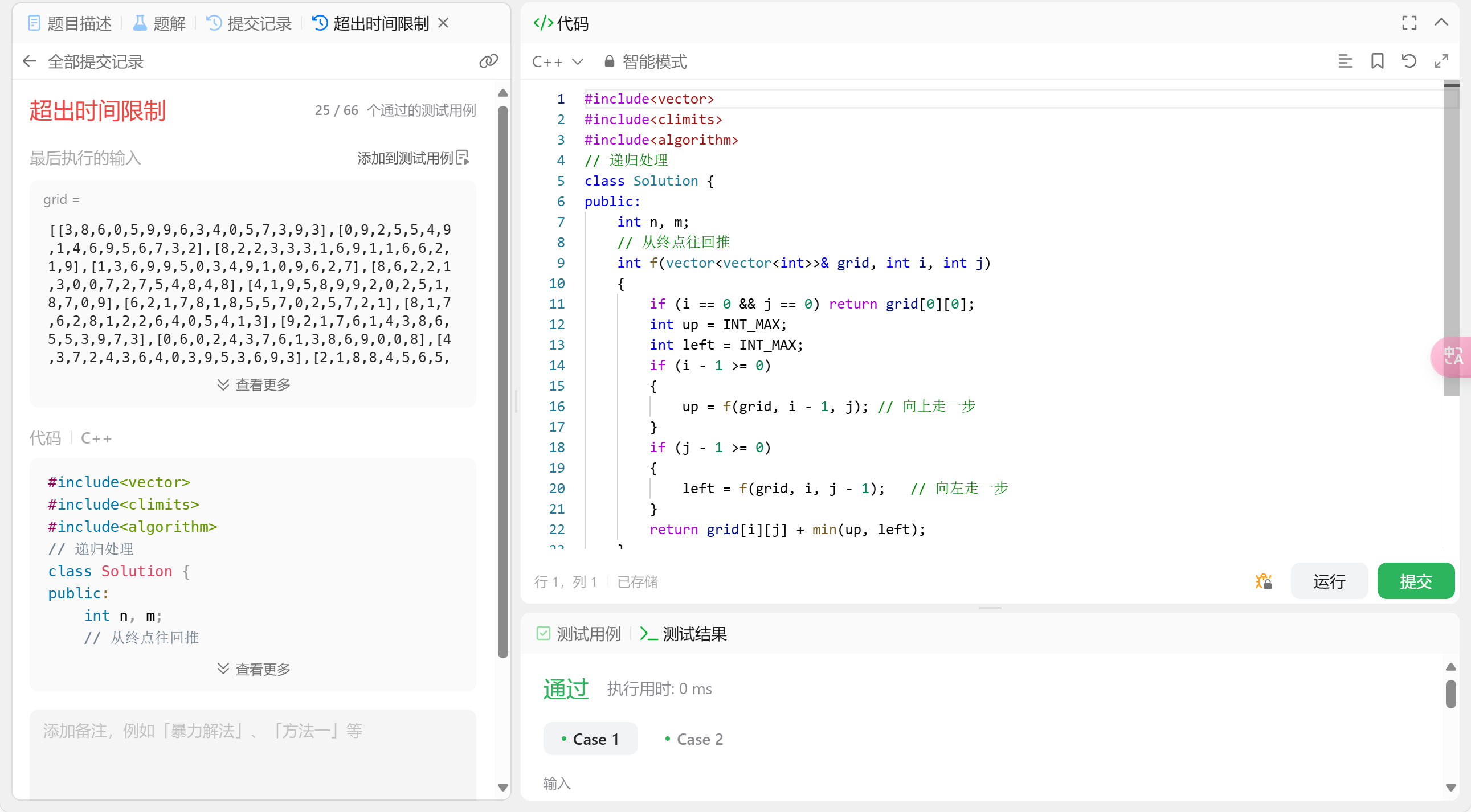
可以看到设计思路没问题但是执行速度非常慢, 因此我们需要用dp优化一下。
2. 做记忆化搜索的dp实现
我决定在递归时使用一个二维dp数组来动态规划, 对每个格子进行结果缓存, 使用记忆化搜索避免重复计算。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include<algorithm>
#include<climits>
class Solution {
public:
// 记忆化搜索
vector<vector<int>> dp;
int n, m;
int f(vector<vector<int>>& grid, int i, int j)
{
if(dp[i][j] != -1)
{
return dp[i][j];
}
int ans;
if(i == 0 && j == 0)
{
ans = grid[0][0];
}
else
{
int up = INT_MAX, left = INT_MAX; // 保证一边无效时, 另外一边是有效的
if(i - 1 >= 0)
{ up = f(grid, i - 1, j); }
if(j - 1 >= 0)
{ left = f(grid, i, j - 1); }
ans = grid[i][j] + min(up, left);
}
dp[i][j] = ans; // 第一次赋值于dp[0][0]
return ans;
}
int minPathSum(vector<vector<int>>& grid) {
n = grid.size();
m = grid[0].size();
dp = vector<vector<int>>(n, vector<int>(m, -1));
return f(grid, n - 1, m - 1);
}
};
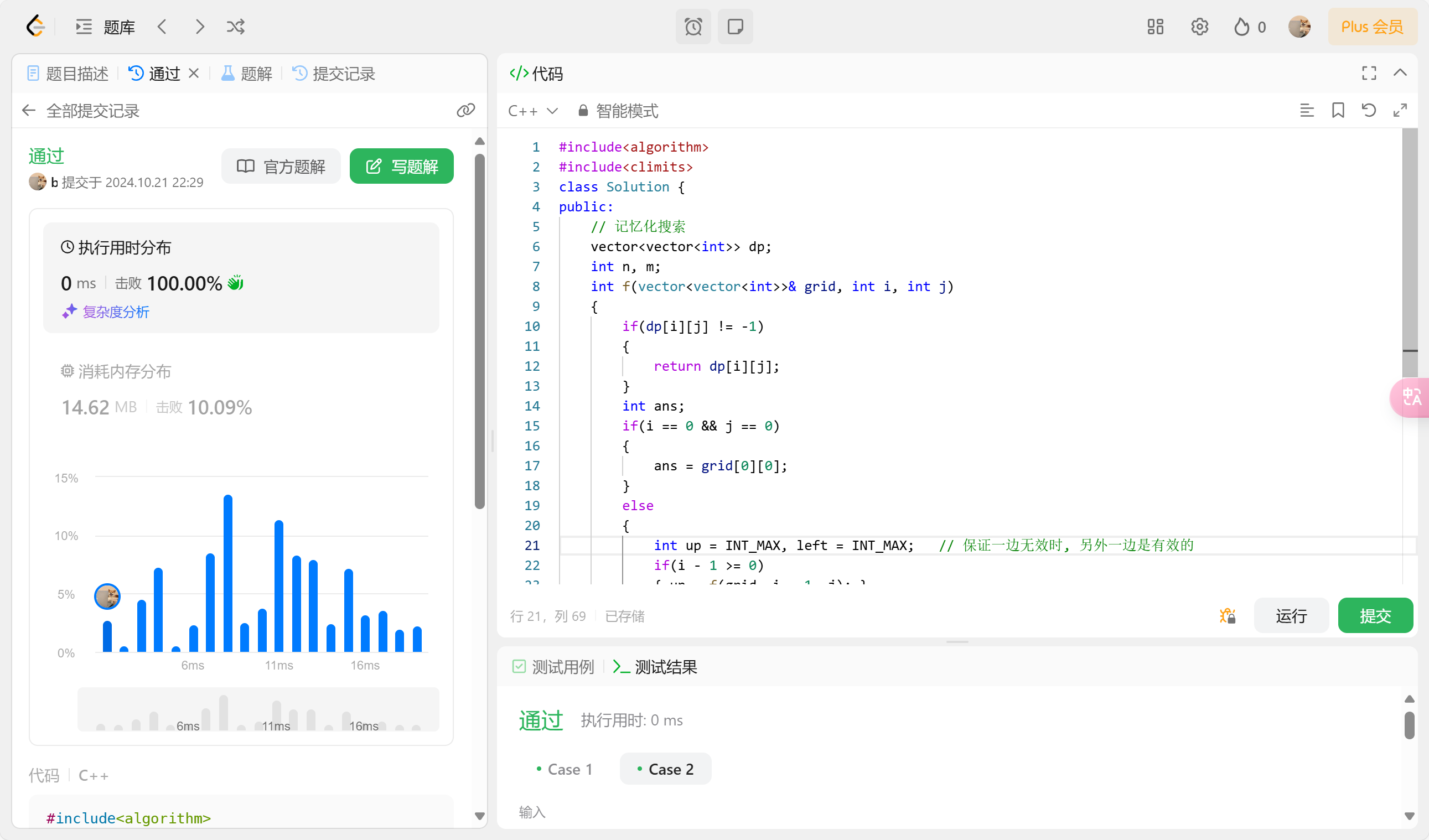
可以看到执行速度快了很多, 但每次递归调用都会带来函数调用的开销,包括参数传递、栈操作等, 因此我们需要继续优化。
3. 做严格位置依赖的dp实现
根据上述的dp实现思路, 我们可以发现dp[i][j]只依赖于dp[i-1][j]和dp[i][j-1], 因此我们可以将将这些dp位置关联起来, 然后使用for循环来实现dp。
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include<algorithm>
#include<climits>
class Solution {
public:
int n, m;
vector<vector<int>> dp;
int minPathSum(vector<vector<int>>& grid) {
n = grid.size();
m = grid[0].size();
if( n == 1 && m == 1)
{
return grid[0][0];
}
dp = vector<vector<int>>(n, vector<int>(m, INT_MAX)); // 0 <= grid[i][j] <= 200
dp[n - 1][m - 1] = grid[n - 1][m - 1];
for(int i = n - 1; i >= 0; --i)
{
for(int j = m - 1; j >= 0; --j)
{
if(i - 1 >= 0) dp[i - 1][j] = min(dp[i - 1][j], dp[i][j] + grid[i - 1][j]); // 向上
if(j - 1 >= 0) dp[i][j - 1] = min(dp[i][j - 1], dp[i][j] + grid[i][j - 1]); // 向左
}
}
return dp[0][0];
}
};
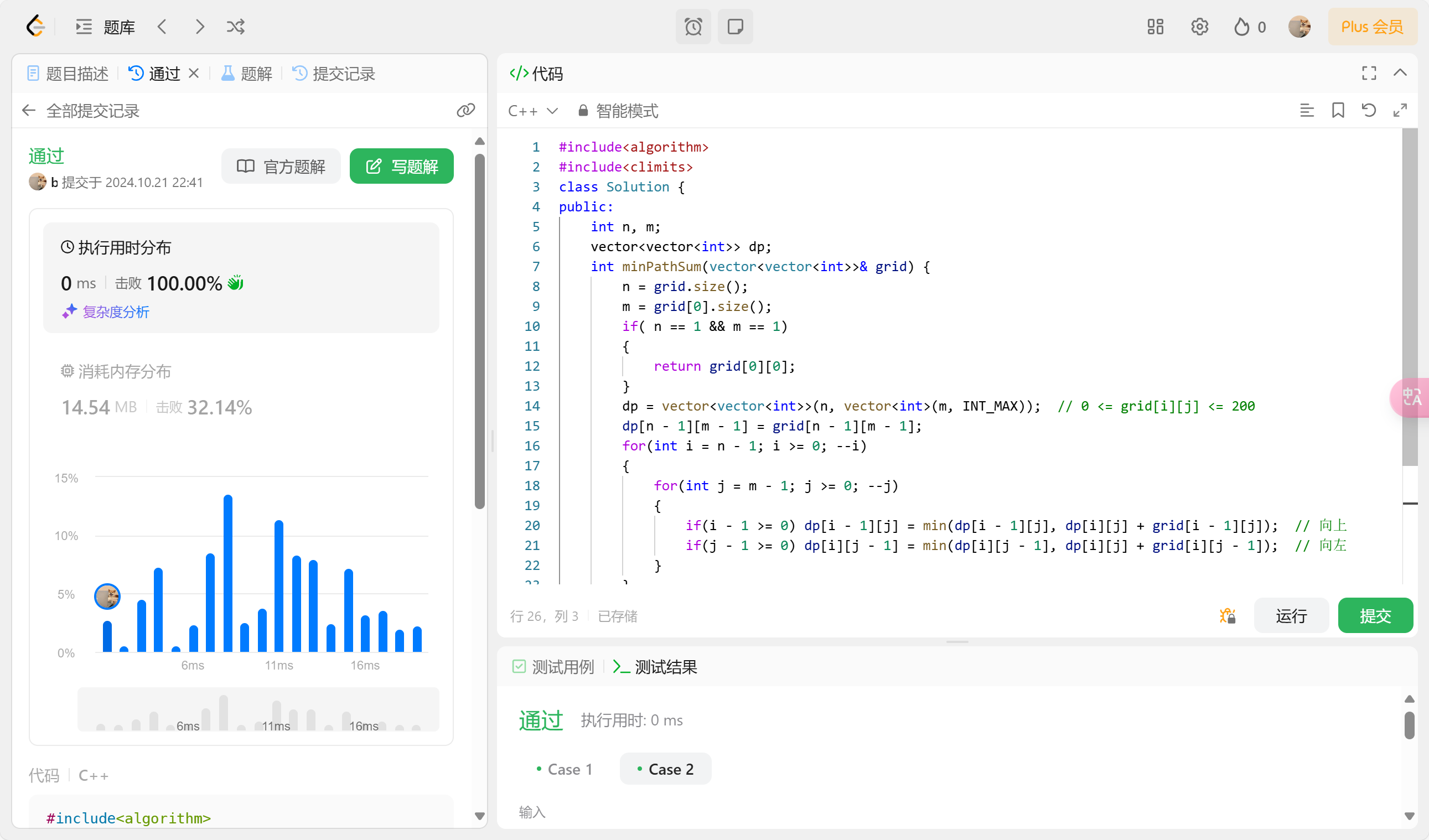
可以看到使用了严格位置依赖后的代码变得更简洁更高效了, 但其内存消耗还是过大, 于是可以进行下一步优化
4. 做空间优化的dp实现
我们会在上述代码中发现dp在后面的过程中只使用了dp[i-1][j]和dp[i][j-1], 因此我们可以使用两个一维dp数组来代替二维dp数组, 从而实现空间优化。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
// 两个dp数组去滚动二维dp, 进行空间压缩
#include<algorithm>
#include<climits>
class Solution {
public:
int n, m;
vector<int> dp1;
vector<int> dp2;
int minPathSum(vector<vector<int>>& grid) {
n = grid.size();
m = grid[0].size();
if (n == 1 && m == 1)
{
return grid[0][0];
}
dp1 = vector<int>(m, INT_MAX); // 0 <= grid[i][j] <= 200
dp2 = vector<int>(m, INT_MAX);
dp1[0] = grid[0][0];
for (int i = 1; i < m; ++i) // 初始化dp1
{
dp1[i] = dp1[i - 1] + grid[0][i];
}
for (int i = 1; i < n; ++i)
{
dp2[0] = dp1[0] + grid[i][0];
for (int j = 1; j < m; ++j)
{
dp2[j] = min(dp1[j], dp2[j - 1]) + grid[i][j];
}
dp1 = dp2;
}
return dp1[m - 1];
}
};
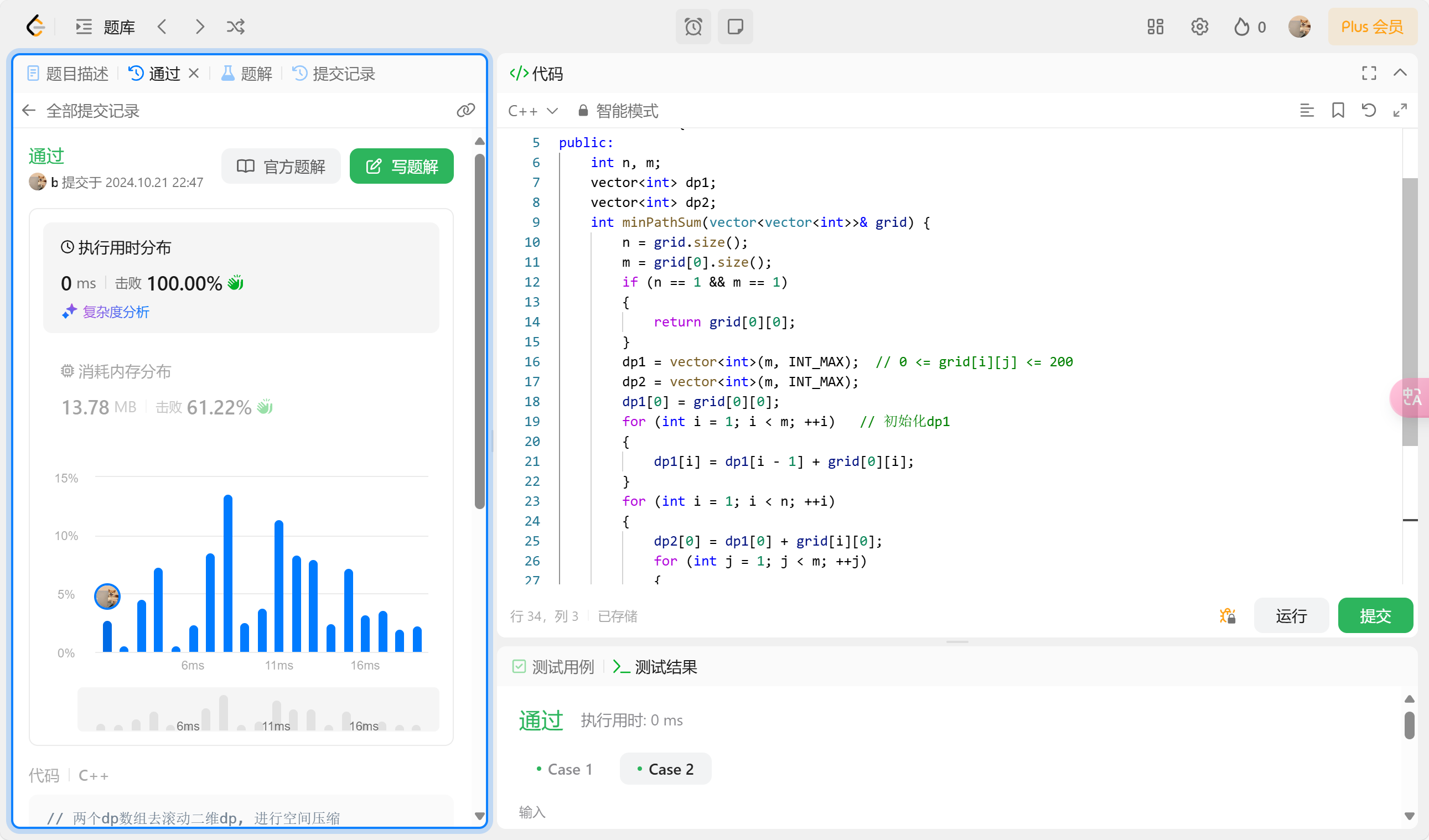
可以看到空间优化后的代码变得消耗的存储更小了, 同时也节省了内存消耗。
总结
从递归到dp, 我认为是dp的最真实实现思路, 其实dp的实现思路并不难, 但要想真正掌握dp的实现思路, 还是需要多思考, 多总结, 多实践。