本文旨在对多重背包问题的算法逻辑进行优化。 本章测试链接 : https://www.luogu.com.cn/problem/P1776
多重背包问题是什么
多重背包是一种介于完全背包和01背包之间的问题，即物品有n种，但是每种物品个数有限。介于这种独特性，多重背包问题的算法逻辑解题思路与这两种背包问题的解决方法密不可分。
多重背包的基础算法逻辑
看到多重背包问题, 我们很容易想到完全背包, 并将其转换成完全背包变体, 测试链接 (这里使用直接空间优化后的多重背包代码, 优化逻辑文章请查看我之前文章):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
vector<int> costs; // 每个宝物需要花费的重量
vector<int> vals; // 每个宝物的价值
vector<int> nums; // 每个宝物的总数量
vector<int> dp; // 当前背包容量 -> 当前价值
int n, m; // 宝物总数, 总背包容量
// 严格位置依赖的空间优化
int compute()
{
dp = vector<int>(m + 1, 0);
// 多重背包
for (int i = 1; i <= n; ++i)
{
for (int j = m; j >= 0; --j) // 防止前面被刷掉
{
// 购买该宝物
for (int t = 1; t <= nums[i] && j - t * costs[i] >= 0; ++t)
{
dp[j] = max(dp[j], dp[j - t * costs[i]] + t * vals[i]);
}
}
}
return dp[m];
}
int main()
{
cin >> n >> m;
costs = vector<int>(n + 1);
vals = vector<int>(n + 1);
nums = vector<int>(n + 1);
for (int i = 1; i <= n; ++i)
{
cin >> vals[i] >> costs[i] >> nums[i];
}
cout << compute();
return 0;
}
提交结果如下 :
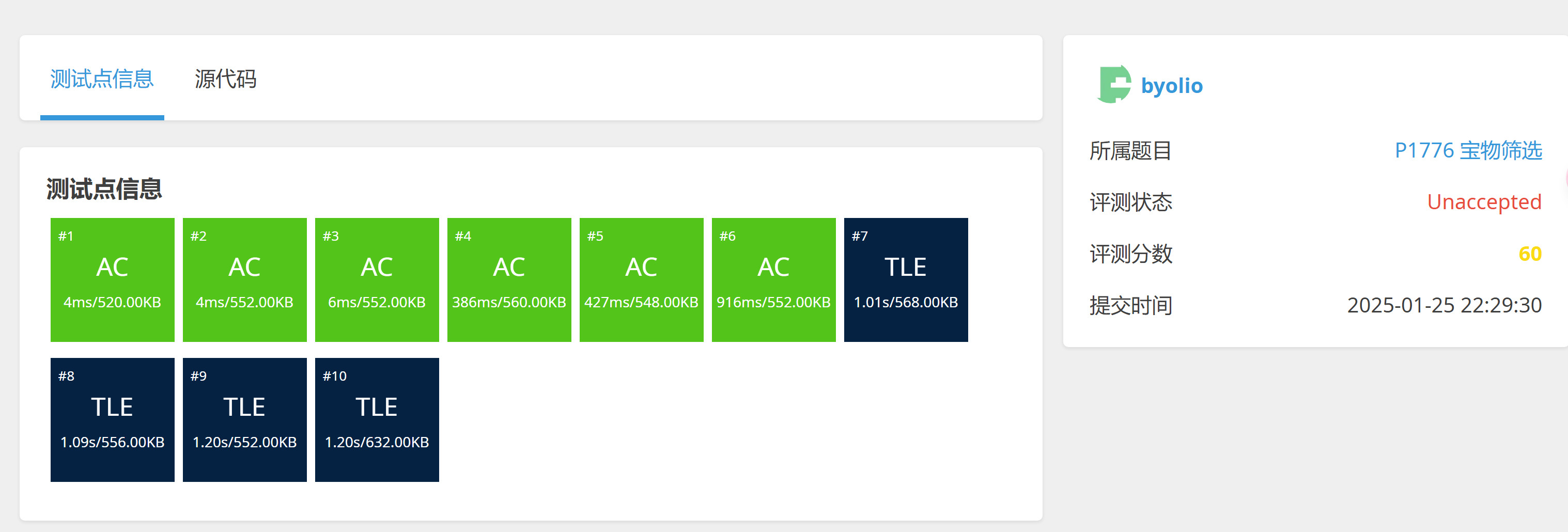可以看到结果TLE(Time Limit Exceeded), 这是因为多重背包问题的时间复杂度为O(N * M * K), 其中N为物品数量, M为背包容量, K为物品个数, 导致时间复杂度过高, 无法通过测试, 因此需要对算法逻辑进行优化。
多重背包的二进制分组算法逻辑
算法逻辑示例
我之前说过, 多重背包问题是介于完全背包和01背包之间的问题, 在完全背包解法时间复杂度过高的情况下, 我们可以将多重背包问题转换成01背包问题, 然后使用01背包问题的算法逻辑进行求解, 先看代码, 测试链接同上(本题如果没有空间优化会导致MLE(Memory Limit Exceeded), 因此需要使用空间优化的版本) :
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
vector<int> costs; // 每个分组中全部花费的重量
vector<int> vals; // 每个分组中全部宝物的价值
vector<int> dp; // 组别idx + 当前背包容量 -> 当前价值
int n, m; // 组总数(01背包中无效), 总背包容量
int len; // 01背包中物品总数
int compute1()
{
dp = vector<int>(m + 1, 0);
// 01背包
for (int i = 1; i <= len; ++i)
{
for (int j = m; j >= costs[i]; --j)
{
dp[j] = max(dp[j], dp[j - costs[i]] + vals[i]);
}
}
return dp[m];
}
int main()
{
cin >> n >> m;
// 做一次冗余
costs = vector<int>(1);
vals = vector<int>(1);
// 数据改写成分组背包
for (int i = 1, v, w, c; i <= n; ++i) // 第1~n组别
{
cin >> v >> w >> c;
for (int j = 1; j <= c; j <<= 1) // 从选择开始, 如不选择就跳过整组
{
costs.push_back(w * j); // 该分组花费
vals.push_back(v * j); // 该分组价值
c -= j;
}
if (c > 0) // 使其不存在大于总数的值, 将分组背包转为01背包
{
costs.push_back(w * c);
vals.push_back(v * c);
}
}
// 完成分组后可以视为01背包
len = vals.size();
cout << compute1();
return 0;
}
结果如下:
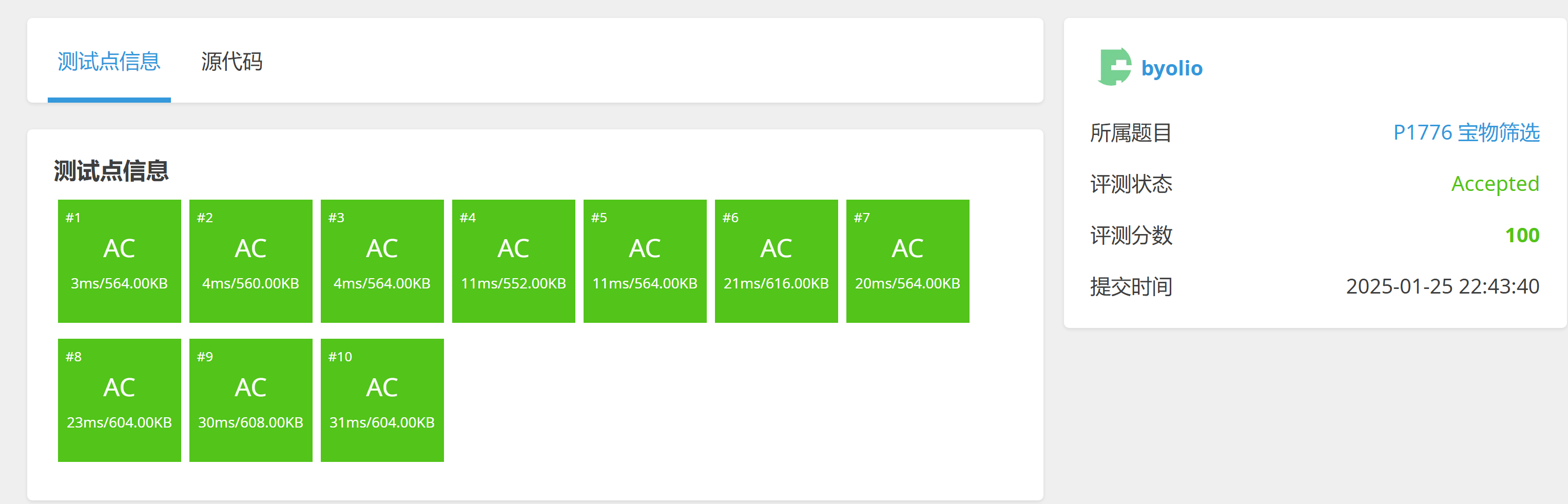全部通过测试!!!
解析二进制分组算法逻辑
在多重背包问题中，每种物品可以选择多个，但不能超过一个组中的最大数量。因此，转换成01背包问题的关键是“分组”策略。不断通过乘以2的方式完成分组, 直到无法再继续分组时, 将剩余部分作为一个单独的组。这样，即使在全部都被选择的情况下仍然小于最大数量, 但却可以通过不同的组合来达到任意数量, 最后将分组后的问题使用01背包问题的算法逻辑进行求解即可。这样可以将其时间复杂度变成O(N * M * logK), 其中N为物品数量, M为背包容量, K为物品个数, 相对于之前的O(N * M * K)时间复杂度有了很大的优化。
多重背包的单调队列算法逻辑
使用二进制分组还是有一个问题, 就是如果物品数量过多, 那么分组后会导致分组数量过多, 从而导致空间复杂度过高, 因此我们需要对算法逻辑进行优化。而单调队列算法逻辑就是一种很好的优化方法, 其可以将时间复杂度优化到O(N * M), 其中N为物品数量, M为背包容量。
试链接同上(使用空间优化版本), 代码如下 :
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
vector<int> costs; // 花费
vector<int> nums; // 数量
vector<int> vals; // 价值
vector<int> dp; // 一维dp
int l, r; // 单调队列指针
int n, t; // 物品种类数和背包容量
int value1(int i, int j) {
return dp[j] - j / costs[i] * vals[i];
}
// 空间优化
int compute()
{
dp = vector<int>(t + 1, 0); // 动态规划数组
deque<int> q; // 使用双端队列实现单调队列
for (int i = 1; i <= n; ++i)
{
for (int mod = 0; mod <= min(t, costs[i] - 1); ++mod) // 最小个数或代价-1, 不同mod下每个添加costs[i]分组
{
q.clear();
for (int j = t - mod, cnt = 1; j >= 0 && cnt <= nums[i]; j -= costs[i], ++cnt) // 取正确位置的值
{
while (!q.empty() && value1(i, q.back()) <= value1(i, j))
{
q.pop_back();
}
q.push_back(j);
}
for (int j = t - mod, enter = j - costs[i] * nums[i]; j >= 0; j -= costs[i], enter -= costs[i])
{
if (enter >= 0)
{
while (!q.empty() && value1(i, q.back()) <= value1(i, enter))
{
q.pop_back();
}
q.push_back(enter);
}
dp[j] = value1(i, q.front()) + j / costs[i] * vals[i];
if (q.front() == j)
{
q.pop_front();
}
}
}
}
return dp[t];
}
int main()
{
cin >> n >> t;
vals = vector<int>(n + 1);
nums = vector<int>(n + 1);
costs = vector<int>(n + 1);
for (int i = 1; i <= n; i++) {
cin >> vals[i] >> costs[i] >> nums[i]; // 输入价值、重量和数量
}
cout << compute();
return 0;
}
这种解法需要使用同余类分组, 因为增加相同余数下可以添加整数倍的代价, 并使用value函数让其规律更加清晰, 在相同上限为j的情况下, 使用单调队列进行优化。
总结
以上就是多重背包问题的三种算法逻辑, 希望对你有所帮助。
